cdestem.com

什么是本福德定律？

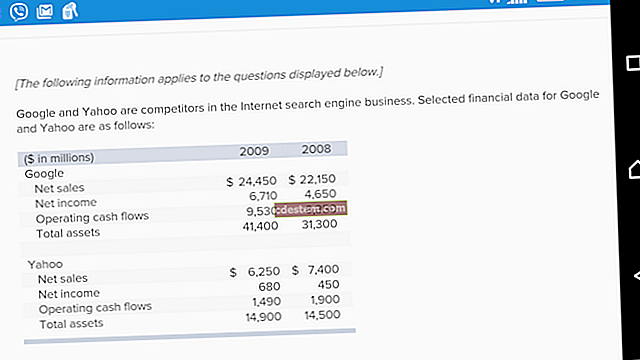
本福德定律指出，在自然出现的一组数字中，较小的数字与前导数字出现的比例不成比例。前导数字具有下表中所示的分布，其中数字1占首位数字的时间略多于30％，数字9表示占首位数字的时间少于5％（即相差6倍）。

1 = 30.1％的发生频率

2 = 17.6％的发生频率

3 =发生频率的12.5％

4 = 9.7％的发生频率

5 = 7.9％的出现频率

6 = 6.7％的发生频率

7 = 5.8％的发生频率

8 = 5.1％的出现频率

9 = 4.6％的发生频率

如果所有数字都以统一的方式显示为前导数字，则每个数字将以大约11.1％的时间出现。由于本福德定律中所述的分配与统一分配所表明的分配之间存在很大差异，因此可以使用这种差异来定位欺诈事件。

分析涉及计算一系列数字中第一个数字的分布。如果分布与本福德定律所规定的比例不同，则可能存在欺诈行为。造成这种差异的原因是，实施欺诈的人会创建随机生成的数字，而不是遵循本福德的分布。

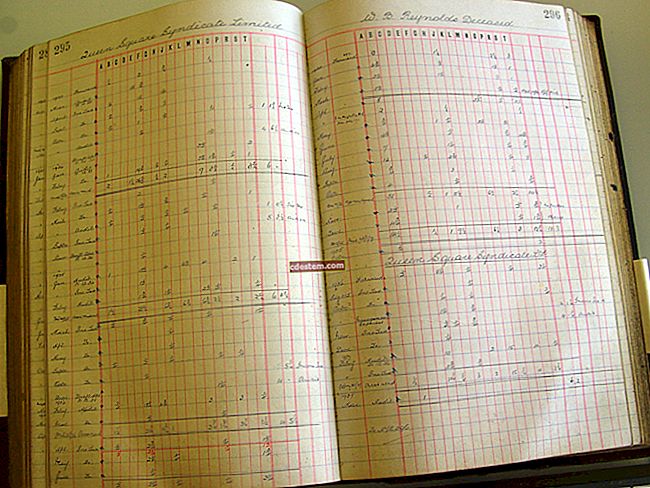
重要的是要了解可以应用本福德定律的情况。频率分布仅适用于自然数。在企业中，这些数字的示例是发票上的总计，产品的汇总成本或库存单位数。它不适用于已分配编号的情况，例如顺序分配的支票编号或发票编号。

本福德定律也被称为第一位数定律。